Kamu Number Theory
| Contents |
|
Preface
|
| Summery |
|
1.Kamu Axiom system
|
|
2.Kamu Dimension system
|
|
3.Space Time compatible Quantum
|
|
4.Topological model of Ama Universe
|
| Kamu Number Theory |
| ver.2019.10 |
| Masaki Yoshino |
| Masaki Yoshino |
| site opned 2019.2.20 |
| studying Similarity schem theory from 1975 |
| copyright (c) 2019 all rights rezerved |
| blog in English and Japanese |
| New pdf 1-1-9.Futomani 1-1-8.Pair Production 1-1-7.Super Duality 1-1-6.Dyad 1-9-1.What is Ka ? 1-9-2.What is Ka & Ma 1-9-3.What is Ma ? |
| Chapter Index |
|
A4 size pdf Plate Index
|
| Preface |
| Summery |
|
|
|
1.Kamu Axiom System
|
|
|
|
1-1.Construction of Axioms
1-1-1.Axiom K and Axiom A 1-1-2.Field with one Element 1-1-3.Kamu Postulate |
|
1-2.Axiom from K1 to K8
1-2-1-1.K1,MaKaTama Symmetry 1-2-1-2.K1,spontaneous symmetry breaking 1-2-1-3.K1,UrForm and Prototype 1-2-2.K2,Mawari & Rotation 1-2-3.K3,differentiation and integration 1-2-4.K4,Kamu addition and multiplication 1-2-5.K5, Tokotachi Super Duality 1-2-6.K6, Pair Production 1-2-7.K7, Futomani 1-2-8.K8,Yata Phenomenon generation Field 1-2-9-1.What is Ka ? 1-2-9-2.What is Ma ? |
| 1-3.Axiom from A1 to A8 1-3-1.A1,Dynamic Saturation Stability 1-3-2.A2,Ama differentiation and integration 1-3-3.A3,Potential automorphic 4 Phases 1-3-4.A4,Tabane & Formal Power Series 1-3-5.A5,Imatachi & logic of Life. 1-3-6.A6, Compatibility and Duality 1-3-7.A7,Oho & Kamu forgetful Functor 1-3-8.A8,Kamuutsusi & Amautsushi |
| 1-4.Symboles inTransition Diaguram 1-4-1.First Reconsider the Operation 1-4-2.Compatible and Polymetric Additive operation 1-4-3.To Caputure Differenntial Integral with a wave image 1-4-4.Tranqull operation and Tropical Geometry |
| 1-5.Potential cuspidal automorphic form 1-5-1.Making an illustration of "Magatama Symmetry" of Axiom K-1 becomes Cuspidal automorphic form 1-5-2. Cuspidal automorphic form genetically dominating "Axiom A" |
| 1-6. Kamu imaginary Diamond and mirror symmetry 1-6-1. |
| 1-7. Axiom K-5 & 6 and the way to Carabi-Yau manifold 1-7-1. |
| 1-8. Carabi-Yau manifold to E8 Transition process and Axioms K8 |
| 1-9. Axiom A and Lie group U (1), SU (2), SU (3) |
| 1-10. Kamu Rosetta Stone |
| 1-11. Kurokawa multiple trigonometric function model |
| 1-12.Relativity-Capacitive-Quantity and Entropy 1-12-1.Reforming Boltzmann's Entropy definition formula and Information Thermodynamics 1-12-2.Guage Space and Relativity-Capacitive-Quantity |
| 1-13. Newton's map Model of Zeta function |
| "If we assume that people who are not Japanese do not know Mu or Ma, then that assumption is a big mistake." says Seigo Matsuoka. (3.March, 2001. Seigo Matsuoka is a leading Japanese writer) https://1000ya.isis.ne.jp/0258.html |
|
| Other than Japanese, there are philosophers who "searched for a place of wisdom and finally found out to know Mu or Ma". Furthermore, S.Matsuoka says, "One of the most cleanest and most courageous of them is Simone Weil." | |
| The philosopher of <Mu or Ma>, which developed in Japan, is considered by many to be understood only by Japanese people.The philosophy of Ma is expressed as music art by the traditional Japanese "Nōgaku". "Nōgaku" is transmitted in Japan as a deep Art with a 1000-years history. |
|
| S.Matsuoka stated such a situation as mentioned above as a premise. S.Well, in the case of a French woman who is one of those who understand Ma besides Japanese. | |
| It is clear that S.Weil had a deep interest in mathematical physics, as well as respect and enthusiasm for his elder brother who is a well-known mathematician. I think that she has evidence that she intuitively understood that "Gravity" is a major issue. |
|
| Simone Weil has shown, as follows, the way of thinking linked to the "Penrose-Narasaki-Nishida contraction principle" surprisingly. (For 1-2-3.Axiom K-3: Nami, Nagi; Derivative and Integral, for the "contraction principle") |
|
| "Creation is not expansion but contraction," S.Weil accurately describes how Ma was created.Furthermore, Simone Weil has explained the necessity of going back to Ka and has shown the idea of "decreation". | |
| So I think you understand why I cited S.Weil here. Originally, S.Weil has a considerable connection with Kamu Number Theory.The Rosetta Stone idea was S. Weil's brother A.Weil, and this idea was first shown in a letter to her sister. | |
| In the 21st century mathematics, the grand unification has been developed in the direction indicated by Rosetta Stone steadily. | |
 |
|
|
|
 |
|
| pdf.What is Ma? |
 |
|
|
|
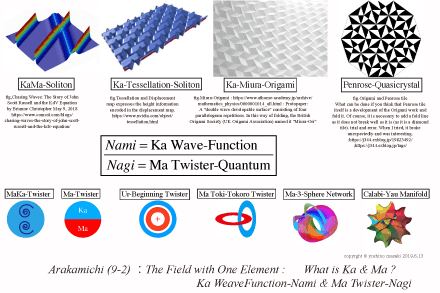
| In the illustration, <Ka> and <Ma> are displayed on the top and bottom in <Mukahi>.There are Crosslinking System and Duality between <Ka> and <Ma>. At the same time, there is also Similarity.Although this complex structure is called UrForm, a number of physical properties are shown on the plate in UrForm. | |
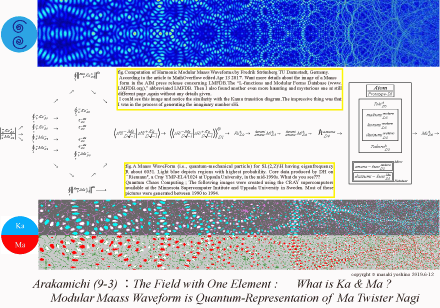
| The computer realizes the desire to visualize such UrForm.In the third plate, the upper row is a plate of <Ka>, and the lower row is a plate of <Ma>.The illustrated plate of the Maass automorphic wave form presented this time is a plate discovered around 2015. | |
| There have already been cusp automorphic forms and Kurokawa multiple trigonometric functions as models of transition diagrams. I think that the five figure appears in the model of transition diagram.The basic form of this model was Maass automorphic wave form. |
| ( I want to see the plate. Transition Diagram 5 Models ) |
| In the pdf figure "What is Ka & Ma", the Twister is the leading role.It was born from Axiom K-2 and Axiom K-3.Twistor was the best choice to satisfy the axiom of the conjugate between Mawari and Meguri. |
| It is unclear whether "3-Sphere" is generated by "physically solving operation" from "Ma Twister".If this transition process is established, the transition from 3-Sphere to Calabi Yau Manifold will be possible.Here, I have to separate Twistor from Penrose Twister and view it as "Ma-twistor".I hope this two twistor matches, but currently unknown. |
|
|
| 1-1-1.Axiom K and Axiom A |
| pdf.A-1-4-2.Overview K & A Axiom Systems |