Kamu Number Theory
| Contents |
|
Preface
|
| Summery |
|
1.Kamu Axiom system
|
|
2.Kamu Dimension system
|
|
3.Space Time compatible Quantum
|
|
4.Topological model of Ama Universe
|
| Kamu Number Theory |
| ver.2019.10 |
| Masaki Yoshino |
| Masaki Yoshino |
| site opned 2019.2.20 |
| studying Similarity schem theory from 1975 |
| copyright (c) 2019 all rights rezerved |
| blog in English and Japanese |
Ma-Ka Compatible-Polymerization
Super Duality
| New pdf 1-1-9.Futomani 1-1-8.Pair Production 1-1-7.Super Duality 1-1-6.Dyad 1-9-1.What is Ka ? 1-9-2.What is Ka & Ma 1-9-3.What is Ma ? |
| Chapter Index |
as UrForm )
|
A4 size pdf Plate Index
|
| Preface |
| Summery |
|
|
|
1.Kamu Axiom System
|
|
|
|
1-1.Construction of Axioms
1-1-1.Axiom K and Axiom A 1-1-2.Field with one Element 1-1-3.Kamu Postulate |
|
1-2.Axiom from K1 to K8
1-2-1-1.K1,MaKaTama Symmetry 1-2-1-2.K1,spontaneous symmetry breaking 1-2-1-3.K1,UrForm and Prototype 1-2-2.K2,Mawari & Rotation 1-2-3.K3,differentiation and integration 1-2-4.K4,Kamu addition and multiplication 1-2-5.K5, Tokotachi Super Duality 1-2-6.K6, Pair Production 1-2-7.K7, Futomani 1-2-8.K8,Yata Phenomenon generation Field 1-2-9-1.What is Ka ? 1-2-9-2.What is Ma ? |
| 1-3.Axiom from A1 to A8 1-3-1.A1,Dynamic Saturation Stability 1-3-2.A2,Ama differentiation and integration 1-3-3.A3,Potential automorphic 4 Phases 1-3-4.A4,Tabane & Formal Power Series 1-3-5.A5,Imatachi & logic of Life. 1-3-6.A6, Compatibility and Duality 1-3-7.A7,Oho & Kamu forgetful Functor 1-3-8.A8,Kamuutsusi & Amautsushi |
| 1-4.Symboles inTransition Diaguram 1-4-1.First Reconsider the Operation 1-4-2.Compatible and Polymetric Additive operation 1-4-3.To Caputure Differenntial Integral with a wave image 1-4-4.Tranqull operation and Tropical Geometry |
| 1-5.Potential cuspidal automorphic form 1-5-1.Making an illustration of "Magatama Symmetry" of Axiom K-1 becomes Cuspidal automorphic form 1-5-2. Cuspidal automorphic form genetically dominating "Axiom A" |
| 1-6. Kamu imaginary Diamond and mirror symmetry 1-6-1. |
| 1-7. Axiom K-5 & 6 and the way to Carabi-Yau manifold 1-7-1. |
| 1-8. Carabi-Yau manifold to E8 Transition process and Axioms K8 |
| 1-9. Axiom A and Lie group U (1), SU (2), SU (3) |
| 1-10. Kamu Rosetta Stone |
| 1-11. Kurokawa multiple trigonometric function model |
| 1-12.Relativity-Capacitive-Quantity and Entropy 1-12-1.Reforming Boltzmann's Entropy definition formula and Information Thermodynamics 1-12-2.Guage Space and Relativity-Capacitive-Quantity |
| 1-13. Newton's map Model of Zeta function |
|
|
| I think the problem of “Wave–particle duality” is an issue that cannot be settled in quantum mechanics. Tokotachi shows that the principle related to the generation of Life is hidden in this duality problem. |
| It is a very important axiom, but it is quite difficult to understand.Therefore, in order to make this axiom easier to understand, we decided to present the mathematical model of Tokotachi. However, not everything is drawn with this model.Originally, the intuition for <Ka> and <Ma> must be the starting point. |
| However, Kamu Number Theory is premised on discussing without entering the world of intuition. I constructed the Tokotachi model based on the axiom system proposed by S.Narasaki. |
| From this model, my immediate task is to show the principles of Life generation and the birth of the Universe. |
| The Dyad form or Tensor shown in Axiom K-4 is represented graphically by changing its form to Toyo.<Toyo> is shown as a figure with four colors divided into four planes. |
| While searching for a figure that could express the physical property of Tokotachi's compatible polymerization, I came across a remarkable figure.That is what the plate shows. |
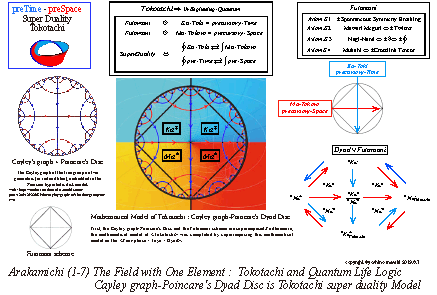 |
| pdf . Arakamichi (1-7) : Axiom K-5 Tokotachi |
| This figure was a Poincare disk and a free group of Cayley graphs. First, the Poincare disk is a form suitable for expressing interchangeable superposition of the infiniteness of <Ka> and the finiteness of <Ma>.The Cayley graph then appears to be compatible with the two generaters <Ka> and <Ma>. |
| And when you superimpose these two, you will be surprised by the fact that a compatible polymerization scheme appears.I overlaid this figure with a Futomani scheme and overlaid with Toyo. |
| By doing so, I thought that Tokotachi's physical properties could be consolidated into a single figure.I named this illustration "Cayley graph Poincaré disc Dyad Tokotachi Model=CPT Model". This is a model of Toyo (Dyad), Futomani, and Tokotachi conjugates. |
| Later, <Toyo> will become an independent axiom as Ama Axiom A-3 of the Ama phenomenon system.In addition, Futomani scheme is shown here as a synthesis of Axiom K-1 to Axiom K-4. |
 |
| But Futomani is an independent axiom as Axiom K-7, so more details will be given later. At this stage, please understand it as a synthesis of the already described axioms as per the plate. |
| To understand Tokotachi's “Latent-Phenomenon physics of compatible superposition”, Toyo (Dyad), Futomani, and Tokotachi are necessary. |
| Why can the “Cayley graph of the free group on two generators (in red and blue), embedded in the Poincaré hyperbolic disk model” express the physics of compatible polymerization in this way? |
| For free groups. I feel that the free group is probably related to the Monoid and also closely related to Adjunction in Category theory. |
| From the viewpoint of similarity, it is speculated that this model hides deep truth.The author of Curiosa Mathematica, Jens Bossaert, is the creator of the plate. |
| "I absolutely adore this picture: it combines so many interesting mathematical ideas (group theory, graph theory, hyperbolic geometry) into a single image!". Yes, I would also like to express my respect for being able to see the origin of Life in this illustration. https://curiosamathematica.tumblr.com/post/120912922685/the-cayley-graph-of-the-free-group-on-two |
|
| Physical properties that are closely related to the generation of life are time.However, <Tokotachi> shows that physical properties are not different in time and space. |
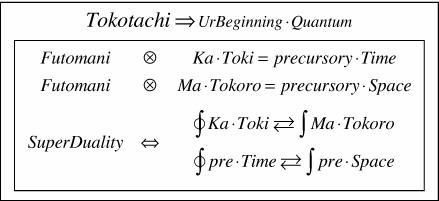 |
| Furthermore, <Tokotachi> creates a precursory-space-time in the Latent world. This is called “Compatible Polymerization Space-time Elementary charge Quantum” and is called “Ur-Beginning Quantum”. |
| This axiom shows that the most primitive Elementary charge Quantum of spacetime is generated. In other words, the first UrForm that appears is the original compatible polymerization spacetime. |
| New pdf 1-1-9.Futomani 1-1-8.Pair Production 1-1-7.Super Duality 1-1-6.Dyad 1-9-1.What is Ka ? 1-9-2.What is Ka & Ma 1-9-3.What is Ma ? |
| Therefore, what is important is how to understand the concept of interchangeable polymerization. As I mentioned at the beginning, it is also a problem of “Wave–particle duality”. |
| This is the physical property of <Tokotachi>, so you can only understand it in modern language except for intuition.I would like to suggest some candidates that I can think of now. |
| Tokotachi = Compatible-Polymerization Super Duality Tokotachi = Superposition of Ma-Ka compatible polymerization Tokotachi = Overlapability of compatible polymerizati Tokotachi = Superposition physical properties of compatible polymerization |
| Tokotachi = Shareability Conjugacy Tokotachi = Separation Conjugacy Tokotachi = Distributed Conjugacy Tokotachi = Separation Conjugacy |
| Tokotachi = Regular-Opposite Duality Tokotachi = Regular-Opposite Superimposed Tokotachi = Regular-Opposite Superposition Tokotachi = Wave–Particle Duality Tokotachi = Ma-Ka Super Duality |
| Tokotachi = MaKa Monoid Tokotachi = MaKa Adjunction |
| And so on. |
|
|
| (Axiom K-5) Tokotachi K-5-1, Kaharikasanari K-5-1, Super Duality K-5-1, Polymerizing-Compatibility K-5-1, Superimposed conjugate coexistence K-5-1, Cumulativeness K-5-1, Ur-Form pattern formation K-5-2, Toyo K-5-2, Four phase of Regular-Opposite-Symmetry K-5-3, Ohoma K-5-3, Macroscopic functional relation K-5-3. Forgetful functor K-5-4, Ohomanowa K-5-4, Renormalization operator K-5-4, Totally bounded operator K-5-4, Precompact operator K-5-5, Power Law |
| New pdf 1-1-9.Futomani 1-1-8.Pair Production 1-1-7.Super Duality 1-1-6.Dyad 1-9-1.What is Ka ? 1-9-2.What is Ka & Ma 1-9-3.What is Ma ? |